publications
publications by categories in reversed chronological order. generated by jekyll-scholar.
2025
-
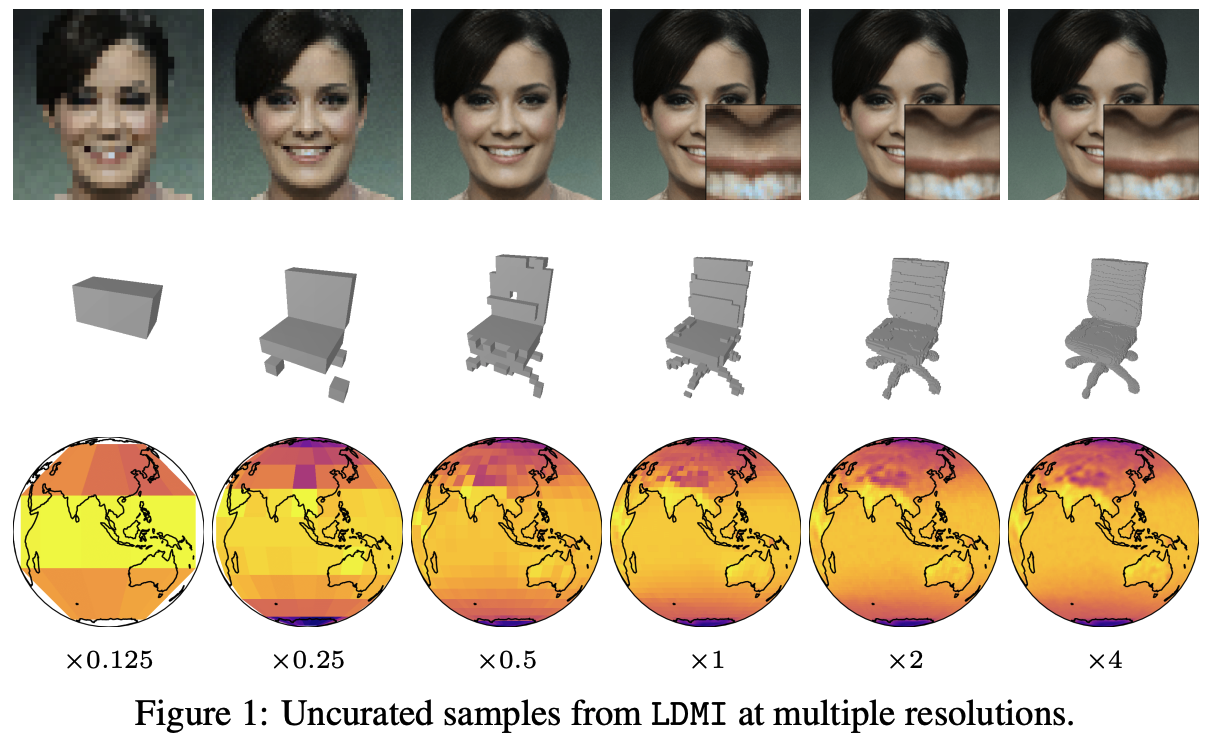 Hyper-Transforming Latent Diffusion ModelsIn Proceedings of the 42nd International Conference on Machine Learning, 13–19 jul 2025
Hyper-Transforming Latent Diffusion ModelsIn Proceedings of the 42nd International Conference on Machine Learning, 13–19 jul 2025We introduce a novel generative framework for functions by integrating Implicit Neural Representations (INRs) and Transformer-based hypernetworks into latent variable models. Unlike prior approaches that rely on MLP-based hypernetworks with scalability limitations, our method employs a Transformer-based decoder to generate INR parameters from latent variables, addressing both representation capacity and computational efficiency. Our framework extends latent diffusion models (LDMs) to INR generation by replacing standard decoders with a Transformer-based hypernetwork, which can be trained either from scratch or via hyper-transforming—a strategy that fine-tunes only the decoder while freezing the pre-trained latent space. This enables efficient adaptation of existing generative models to INR-based representations without requiring full retraining. We validate our approach across multiple modalities, demonstrating improved scalability, expressiveness, and generalization over existing INR-based generative models. Our findings establish a unified and flexible framework for learning structured function representations.
@inproceedings{peis2025hyper, title = {Hyper-Transforming Latent Diffusion Models}, author = {Peis, Ignacio and Koyuncu, Batuhan and Valera, Isabel and Frellsen, Jes}, booktitle = {Proceedings of the 42nd International Conference on Machine Learning}, pages = {48714--48733}, year = {2025}, editor = {Singh, Aarti and Fazel, Maryam and Hsu, Daniel and Lacoste-Julien, Simon and Berkenkamp, Felix and Maharaj, Tegan and Wagstaff, Kiri and Zhu, Jerry}, volume = {267}, series = {Proceedings of Machine Learning Research}, month = {13--19 Jul}, publisher = {PMLR}, url = {https://proceedings.mlr.press/v267/peis25a.html}, bibtex_show = true, selected = true }
2024
- Scalable physical source-to-field inference with hypernetworksBerian James, Stefan Pollok, Ignacio Peis, Jes Frellsen, and Rasmus BjørkarXiv preprint arXiv:2405.05981, 13–19 jul 2024
We present a generative model that amortises computation for the field around e.g. gravitational or magnetic sources. Exact numerical calculation has either computational complexity O(M×N) in the number of sources and field evaluation points, or requires a fixed evaluation grid to exploit fast Fourier transforms. Using an architecture where a hypernetwork produces an implicit representation of the field around a source collection, our model instead performs as (M+N), achieves accuracy of ∼4%−6%, and allows evaluation at arbitrary locations for arbitrary numbers of sources, greatly increasing the speed of e.g. physics simulations. We also examine a model relating to the physical properties of the output field and develop two-dimensional examples to demonstrate its application.
@article{james2024scalable, title = {Scalable physical source-to-field inference with hypernetworks}, author = {James, Berian and Pollok, Stefan and Peis, Ignacio and Frellsen, Jes and Bj{\o}rk, Rasmus}, journal = {arXiv preprint arXiv:2405.05981}, year = {2024}, bibtex_show = true, }
2023
- PhD Thesis
 Advanced Inference and Representation Learning Methods in Variational AutoencodersIgnacio PeisPhD Thesis Dissertation, 13–19 jul 2023
Advanced Inference and Representation Learning Methods in Variational AutoencodersIgnacio PeisPhD Thesis Dissertation, 13–19 jul 2023Deep Generative Models have gained significant popularity in the Machine Learning research community since the early 2010s. These models allow to generate realistic data by leveraging the power of Deep Neural Networks. The field experienced a significant breakthrough when Variational Autoencoders (VAEs) were introduced. VAEs revolutionized Deep Generative Modeling by providing a scalable and flexible framework that enables the generation of complex data distributions and the learning of potentially interpretable latent representations. They have proven to be a powerful tool in numerous applications, from image, sound and video generation to natural language processing or drug discovery, among others. At their core, VAEs encode natural information into a reduced latent space and decode the learned latent space into new synthetic data. Advanced versions of VAEs have been developed to handle challenges such as handling heterogeneous incomplete data, encoding into hierarchical latent spaces for representing abstract and richer concepts, or modeling sequential data, among others. These advances have expanded the capabilities of VAEs and made them a valuable tool in a wide range of fields. Despite the significant progress made in VAE research, there is still ample room for improvement in their current state-of-the-art. One of the major challenges is improving their approximate inference. VAEs typically assume Gaussian approximations of the posterior distribution of the latent variables in order to make the training objective tractable. The parameters of this approximation are provided by encoder networks. However, this approximation leads to a lower bounded objective, which can degrade the performance of any task that requires samples from the approximate posterior, due to the implicit bias. The second major challenge addressed in this thesis is related to achieving meaningful latent representations, or more broadly, how the latent space disentangles generative factors of variation. Ideally, the latent space would modulate meaningful properties separately within each dimension. However, Maximum Likelihood optimizations require the marginalization of latent variables, leading to non-unique solutions that may or may not achieve this desired disentanglement. Additionally, properties learned at the observation level in VAEs assume that every observation is generated independently, which may not be the case in some scenarios. To address these limitations, more robust VAEs have been developed to learn disentangled properties at the supervised group (also referred to as global) level. These models are capable of generating groups of data with shared properties. The work presented in this doctoral thesis focuses on the development of novel methods for improving the state-of-the-art in VAEs. Specifically, three fundamental challenges are addressed: achieving meaningful global latent representations, obtaining highly-flexible priors for learning more expressive models, and improving current approximate inference methods. As a first main contribution, an innovative technique named UG-VAE from Unsupervised-Global VAE, aims to enhance the ability of VAEs in capturing factors of variations at data (local) and group (global) level. By carefully desigining the encoder and the decoder, and throughout conductive experiments, it is demonstrated that UG-VAE is effective in capturing unsupervised global factors from images. Second, a non-trivial combination of highly-expressive Hierarchical VAEs with robust Markov Chain Monte Carlo inference (specifically Hamiltonian Monte Carlo), for which important issues are successfully resolved, is presented. The resulting model, referred to as the Hierarchical Hamiltonian VAE model for Mixed-type incomplete data (HH-VAEM), addresses the challenges associated with imputing and acquiring heterogeneous missing data. Throughout extensive experiments, it is demonstrated that HH-VAEM outperforms existing one-layered and Gaussian baselines in the tasks of missing data imputation and supervised learning with missing features, thanks to its improved inference and expressivity. Furthermore, another relevant contribution is presented, namely a sampling-based approach for efficiently computing the information gain when missing features are to be acquired with HH-VAEM. This approach leverages the advantages of HH-VAEM and is demonstrated to be effective in the same tasks.
@article{peis2023advanced, title = {Advanced Inference and Representation Learning Methods in Variational Autoencoders}, author = {Peis, Ignacio}, journal = {PhD Thesis Dissertation}, year = {2023}, selected = false, bibtex_show = true } - Variational Mixture of HyperGenerators for Learning Distributions Over FunctionsIn Proceedings of the 40th International Conference on Machine Learning, 13–19 jul 2023
Recent approaches build on implicit neural representations (INRs) to propose generative models over function spaces. However, they are computationally intensive when dealing with inference tasks, such as missing data imputation, or directly cannot tackle them. In this work, we propose a novel deep generative model, named VAMoH. VAMoH combines the capabilities of modeling continuous functions using INRs and the inference capabilities of Variational Autoencoders (VAEs). In addition, VAMoH relies on a normalizing flow to define the prior, and a mixture of hypernetworks to parametrize the data log-likelihood. This gives VAMoH a high expressive capability and interpretability. Through experiments on a diverse range of data types, such as images, voxels, and climate data, we show that VAMoH can effectively learn rich distributions over continuous functions. Furthermore, it can perform inference-related tasks, such as conditional super-resolution generation and in-painting, as well or better than previous approaches, while being less computationally demanding.
@inproceedings{koyuncu2023variational, title = {Variational Mixture of HyperGenerators for Learning Distributions Over Functions}, author = {Koyuncu, Batuhan and Sanchez-Martin, Pablo and Peis, Ignacio and Olmos, Pablo M. and Valera, Isabel}, booktitle = {Proceedings of the 40th <b>International Conference on Machine Learning</b>}, year = {2023}, selected = true, bibtex_show = true }
2022
- Missing Data Imputation and Acquisition with Deep Hierarchical Models and Hamiltonian Monte CarloIgnacio Peis, Chao Ma, and José Miguel Hernández-LobatoIn Advances in Neural Information Processing Systems 35, 13–19 jul 2022
Variational Autoencoders (VAEs) have recently been highly successful at imputing and acquiring heterogeneous missing data. However, within this specific application domain, existing VAE methods are restricted by using only one layer of latent variables and strictly Gaussian posterior approximations. To address these limitations, we present HH-VAEM, a Hierarchical VAE model for mixed-type incomplete data that uses Hamiltonian Monte Carlo with automatic hyper-parameter tuning for improved approximate inference. Our experiments show that HH-VAEM outperforms existing baselines in the tasks of missing data imputation and supervised learning with missing features. Finally, we also present a sampling-based approach for efficiently computing the information gain when missing features are to be acquired with HH-VAEM. Our experiments show that this sampling-based approach is superior to alternatives based on Gaussian approximations.
@inproceedings{peis2022missing, title = {Missing Data Imputation and Acquisition with Deep Hierarchical Models and Hamiltonian Monte Carlo}, author = {Peis, Ignacio and Ma, Chao and Hern{\'a}ndez-Lobato, Jos{\'e} Miguel}, booktitle = {Advances in <b>Neural Information Processing Systems</b> 35}, year = {2022}, selected = true, bibtex_show = true } - Unsupervised learning of global factors in deep generative modelsIgnacio Peis, Pablo M. Olmos, and Antonio Artés-RodríguezPattern Recognition, 13–19 jul 2022
We present a novel deep generative model based on non i.i.d. variational autoencoders that captures global dependencies among observations in a fully unsupervised fashion. In contrast to the recent semi-supervised alternatives for global modeling in deep generative models, our approach combines a mixture model in the local or data-dependent space and a global Gaussian latent variable, which lead us to obtain three particular insights. First, the induced latent global space captures interpretable disentangled representations with no user-defined regularization in the evidence lower bound (as in β-VAE and its generalizations). Second, we show that the model performs domain alignment to find correlations and interpolate between different databases. Finally, we study the ability of the global space to discriminate between groups of observations with non-trivial underlying structures, such as face images with shared attributes or defined sequences of digits images.
@article{PEIS2023109130, title = {Unsupervised learning of global factors in deep generative models}, journal = {Pattern Recognition}, volume = {134}, pages = {109130}, year = {2022}, issn = {0031-3203}, doi = {https://doi.org/10.1016/j.patcog.2022.109130}, author = {Peis, Ignacio and Olmos, Pablo M. and Artés-Rodríguez, Antonio}, bibtex_show = true, }
2020
- Actigraphic recording of motor activity in depressed inpatients: a novel computational approach to prediction of clinical course and hospital dischargeIgnacio Peis, Javier-David López-Morı́ñigo, M Mercedes Pérez-Rodrı́guez, Maria-Luisa Barrigón, Marta Ruiz-Gómez, Antonio Artés-Rodríguez, and Enrique Baca-Garcı́aScientific reports, 13–19 jul 2020
Depressed patients present with motor activity abnormalities, which can be easily recorded using actigraphy. The extent to which actigraphically recorded motor activity may predict inpatient clinical course and hospital discharge remains unknown. Participants were recruited from the acute psychiatric inpatient ward at Hospital Rey Juan Carlos (Madrid, Spain). They wore miniature wrist wireless inertial sensors (actigraphs) throughout the admission. We modeled activity levels against the normalized length of admission—‘Progress Towards Discharge’ (PTD)—using a Hierarchical Generalized Linear Regression Model. The estimated date of hospital discharge based on early measures of motor activity and the actual hospital discharge date were compared by a Hierarchical Gaussian Process model. Twenty-three depressed patients (14 females, age: 50.17 ± 12.72 years) were recruited. Activity levels increased during the admission (mean slope of the linear function: 0.12 ± 0.13). For n = 18 inpatients (78.26%) hospitalised for at least 7 days, the mean error of Prediction of Hospital Discharge Date at day 7 was 0.231 ± 22.98 days (95% CI 14.222–14.684). These n = 18 patients were predicted to need, on average, 7 more days in hospital (for a total length of stay of 14 days) (PTD = 0.53). Motor activity increased during the admission in this sample of depressed patients and early patterns of actigraphically recorded activity allowed for accurate prediction of hospital discharge date.
@article{peis2020actigraphic, title = {Actigraphic recording of motor activity in depressed inpatients: a novel computational approach to prediction of clinical course and hospital discharge}, author = {Peis, Ignacio and L{\'o}pez-Mor{\'\i}{\~n}igo, Javier-David and P{\'e}rez-Rodr{\'\i}guez, M Mercedes and Barrig{\'o}n, Maria-Luisa and Ruiz-G{\'o}mez, Marta and Artés-Rodríguez, Antonio and Baca-Garc{\'\i}a, Enrique}, journal = {Scientific reports}, volume = {10}, number = {1}, pages = {1--11}, year = {2020}, publisher = {Nature Publishing Group}, bibtex_show = true }
2019
- Deep sequential models for suicidal ideation from multiple source dataIgnacio Peis, Pablo M. Olmos, Constanza Vera-Varela, Marı́a Luisa Barrigón, Philippe Courtet, Enrique Baca-Garcia, and Antonio Artés-RodríguezIEEE Journal of Biomedical and Health Informatics, 13–19 jul 2019
This paper presents a novel method for predicting suicidal ideation from electronic health records (EHR) and ecological momentary assessment (EMA) data using deep sequential models. Both EHR longitudinal data and EMA question forms are defined by asynchronous, variable length, randomly sampled data sequences. In our method, we model each of them with a recurrent neural network, and both sequences are aligned by concatenating the hidden state of each of them using temporal marks. Furthermore, we incorporate attention schemes to improve performance in long sequences and time-independent pre-trained schemes to cope with very short sequences. Using a database of 1023 patients, our experimental results show that the addition of EMA records boosts the system recall to predict the suicidal ideation diagnosis from 48.13% obtained exclusively from EHR-based state-of-the-art methods to 67.78%. Additionally, our method provides interpretability through the t-distributed stochastic neighbor embedding (t-SNE) representation of the latent space. Furthermore, the most relevant input features are identified and interpreted medically.
@article{peis2019deep, title = {Deep sequential models for suicidal ideation from multiple source data}, author = {Peis, Ignacio and Olmos, Pablo M. and Vera-Varela, Constanza and Barrig{\'o}n, Mar{\'\i}a Luisa and Courtet, Philippe and Baca-Garcia, Enrique and Artés-Rodríguez, Antonio}, journal = {IEEE Journal of Biomedical and Health Informatics}, volume = {23}, number = {6}, pages = {2286--2293}, year = {2019}, publisher = {IEEE}, selected = false, bibtex_show = true }
2017
- A heavy tailed expectation maximization hidden markov random field model with applications to segmentation of MRIDiego Castillo-Barnes, Ignacio Peis, Francisco J Martı́nez-Murcia, Fermı́n Segovia, Ignacio A. Illán, Juan M. Górriz, Javier Ramı́rez, and Diego Salas-GonzalezFrontiers in Neuroinformatics, 13–19 jul 2017
A wide range of segmentation approaches assumes that intensity histograms extracted from magnetic resonance images (MRI) have a distribution for each brain tissue that can be modeled by a Gaussian distribution or a mixture of them. Nevertheless, intensity histograms of White Matter and Gray Matter are not symmetric and they exhibit heavy tails. In this work, we present a hidden Markov random field model with expectation maximization (EM-HMRF) modeling the components using the α-stable distribution. The proposed model is a generalization of the widely used EM-HMRF algorithm with Gaussian distributions. We test the α-stable EM-HMRF model in synthetic data and brain MRI data. The proposed methodology presents two main advantages: Firstly, it is more robust to outliers. Secondly, we obtain similar results than using Gaussian when the Gaussian assumption holds. This approach is able to model the spatial dependence between neighboring voxels in tomographic brain MRI.
@article{castillo2017heavy, title = {A heavy tailed expectation maximization hidden markov random field model with applications to segmentation of MRI}, author = {Castillo-Barnes, Diego and Peis, Ignacio and Mart{\'\i}nez-Murcia, Francisco J and Segovia, Ferm{\'\i}n and Ill{\'a}n, Ignacio A. and G{\'o}rriz, Juan M. and Ram{\'\i}rez, Javier and Salas-Gonzalez, Diego}, journal = {Frontiers in Neuroinformatics}, volume = {11}, pages = {66}, year = {2017}, publisher = {Frontiers}, bibtex_show = true }
2016
- MRI brain segmentation using hidden Markov random fields with alpha-stable distributionsIgnacio Peis, Francisco J. Martı́nez-Murcia, Fermín Segovia, Juan M. Górriz, Javier Ramı́rez, Elmar W. Lang, and Diego Salas-GonzalezIn 2016 IEEE Nuclear Science Symposium, Medical Imaging Conference and Room-Temperature Semiconductor Detector Workshop (NSS/MIC/RTSD), 13–19 jul 2016
A MRI brain image segmentation method using a hidden Markov random fields with heavy-tailed alpha-stable distributions is presented. Each brain tissue is modelled using an alpha-stable distribution. Then, a HMRF is used to include spatial information in the classification model. The Gaussian distribution has been widely used for the modelization of the cerebrospinal fluid, white matter and gray matter. Nevertheless, the alpha-stable distribution has been recently proposed as a more accurate alternative for this task. The alpha-stable distribution is more impulsive and is also able to model the asymmetry and heavy-tails of the histogram of the brain tissues. We have tested the proposed methodology in 18 MR images from the Internet Brain Segmentation Repository. The proposed methodology outperforms the segmentation results obtained when a Gaussian model for the histogram of the brain tissues is considered. Furthermore, as the Normal distribution is a particulaar case of alpha-stable distribution. Therefore, the proposed approach is also a generalization of the hidden Markov random field segmentation method with Gaussian distributions.
@inproceedings{peis2016mri, title = {MRI brain segmentation using hidden Markov random fields with alpha-stable distributions}, author = {Peis, A. Ill{\'a}n, Ignacio and Mart{\'\i}nez-Murcia, Francisco J. and Segovia, Fermín and G{\'o}rriz, Juan M. and Ram{\'\i}rez, Javier and Lang, Elmar W. and Salas-Gonzalez, Diego}, booktitle = {2016 IEEE Nuclear Science Symposium, Medical Imaging Conference and Room-Temperature Semiconductor Detector Workshop (NSS/MIC/RTSD)}, pages = {1--3}, year = {2016}, organization = {IEEE}, bibtex_show = true }